সুনির্দিষ্ট এবং অনির্দিষ্ট সমার্থক পার্থক্য

ক্যালকুলাস গণিতের একটি গুরুত্বপূর্ণ শাখা হিসেবে পরিচিত এবং বিভেদটি ক্যালকুলাসে গুরুত্বপূর্ণ ভূমিকা পালন করে। পার্থক্য এর বিপরীত প্রক্রিয়া ইন্টিগ্রেশন হিসাবে পরিচিত হয়, এবং ইনভার্ট অবিচ্ছেদ্য হিসাবে পরিচিত হয়, বা কেবল করা, বিভেদ বিপরীত একটি অবিচ্ছেদ্য দেয়। তারা ফলিত ফলাফল উপর ভিত্তি করে উভয় ক্লাস বিভক্ত হয় যথা, নিশ্চিত এবং অনিশ্চয়তা

সুনির্দিষ্ট ইন্টিগ্রাল

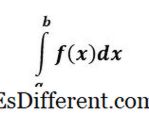
f (x) এর একটি নির্দিষ্ট অবিচ্ছেদ্য নম্বর এবং বক্ররেখাটি f (x) থেকে x = a X = খ এ।

একটি সুনির্দিষ্ট ইন্টিগ্রালের উপর ভিত্তি করে ঊর্ধ্ব ও নিম্ন সীমাবদ্ধতা রয়েছে, এবং এটি অবশ্যই নির্দিষ্ট কারণ, সমস্যা শেষে, আমাদের একটি সংখ্যা আছে - এটি একটি নির্দিষ্ট উত্তর।

--২ ->

অনির্দিষ্ট ইন্টিগ্রাল

F (অ) এর অনির্দিষ্ট ইন্টিগ্রালটি একটি ফাংশন এবং প্রশ্নের উত্তর দেয়, "পার্থক্যটি যখন কাজ করে তখন f (x) কি দেয়? " অবিচ্ছিন্ন অবিচ্ছেদ্য অংশে এখানে অবিচ্ছেদ্য অংশে ঊর্ধ্ব ও নিচু সীমা নেই এবং আমরা যা পাই তা হল একটি উত্তর যা এখনও

x এর মধ্যে রয়েছে এবং এটি একটি ধ্রুবকও থাকবে (সাধারণত এটি সি দ্বারা চিহ্নিত।

অনির্দিষ্ট অবিচ্ছেদ্যভাবে ডিফারাল সমীকরণের সাধারণ সমাধান দেয়।

অনির্দিষ্ট ইন্টিগ্রাল একীকরণের একটি সাধারণ রূপের অধিক, এবং এটি বিবেচিত ফাংশনের বিরোধী ডেরিভেটিভ হিসাবে ব্যাখ্যা করা যেতে পারে।

ফাংশনের বিভেদ অনুমান করা

F অন্য ফাংশন ফ এর দিকে পরিচালিত করে, এবং এফ এর ইন্টিগ্রেশনটি অবিচ্ছেদ্য অংশ দেয়। প্রতীকীভাবে, এটি F (x) = ∫ƒ (x) dx

বা

F = ∫ƒ dx

যেখানে উভয়

F এবং ƒ < এক্স এবং F এর ফাংশনটি ভিন্ন। উপরের রূপে, এটি একটি রিমেন ইন্টিগ্রেলেল এবং এর ফলে ফাংশনটি একটি অবাধ ধ্রুবকটির সাথে যুক্ত হয়। একটি অনিশ্চিত অবিচ্ছেদ্য প্রায়ই ফাংশন একটি পরিবার উত্পাদন; অতএব, অবিচ্ছেদ্য অবিচ্ছেদ্য ইন্টিগ্রালস এবং ইন্টিগ্রেশন প্রক্রিয়ায় ডিফারাল সমীকরণ সমাধানের কেন্দ্রবিন্দু হয়। যাইহোক, পার্থক্য পদক্ষেপের মতন, ইন্টিগ্রেশন পদক্ষেপ সবসময় একটি পরিষ্কার এবং মান রুটিন অনুসরণ না। মাঝে মাঝে, আমরা দেখতে পারি যে সমাধানটি প্রাথমিক ফাংশনের শর্তে প্রকাশ করা যায় না। যে ক্ষেত্রে, বিশ্লেষণের সমাধান প্রায়ই একটি অনির্দিষ্ট অবিচ্ছেদ্য রূপে দেওয়া হয়।

ক্যালকুলাসের মৌলিক উপপাদ্য

নিখুঁত এবং অনির্দিষ্ট অবিচ্ছেদ্য ক্যালকুলাসের মৌলিক উপপাদ্য দ্বারা সংযুক্ত হয়: একটি

নির্দিষ্ট ইন্টিগ্রাল

গণনা করার জন্য, অনির্দিষ্ট অবিচ্ছেদ্য খুঁজে বের করুন > ফাংশনের (এছাড়াও অ্যান্টি-ডেরিভেটিভ হিসাবে পরিচিত)> ওপেন পয়েন্টগুলি x = a এবং x = b এ মূল্যায়ন করুন। একই ফাংশনটির জন্য আমরা সংখ্যাগরিষ্ঠদের মূল্যায়ন করার পরে সুনির্দিষ্ট এবং অনির্দিষ্ট অস্তিত্বের মধ্যে পার্থক্য স্পষ্ট হবে। নীচের অবিচ্ছেদ্য অংশগুলি বিবেচনা করুন: ঠিক আছে। তাদের উভয় না এবং পার্থক্য দেখতে যাক।

ইন্টিগ্রেশন জন্য, আমরা নিম্নলিখিত অভিব্যক্তি আমাদের নেতৃস্থানীয় যা সূচক যা এক যোগ করা প্রয়োজন:

এই সময়ে সময়ে

সি

আমাদের জন্য শুধুমাত্র একটি ধ্রুবক হয়।

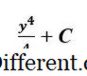
C এর সুনির্দিষ্ট মূল্য নির্ধারণের জন্য অতিরিক্ত তথ্যের জন্য প্রয়োজনীয় তথ্য প্রয়োজন। আসুন আমরা এর সুনির্দিষ্ট ফর্মের একই অবিচ্ছেদ্য মূল্যায়ন করি। ঙ।, ঊর্ধ্ব এবং নিম্ন সীমা সহ অন্তর্ভুক্ত। গ্রাফিক্যালভাবে বলছি, আমরা এখন বক্ররেখাটি f (x) = y

3

এর মধ্যে y = 2 ^এবং y = 3 এর অধীন এলাকা গণনা করছি >। এই মূল্যায়নের প্রথম ধাপ হল অবিচ্ছিন্ন অবিচ্ছেদ্য মূল্যায়ন হিসাবে একই। একমাত্র পার্থক্য হল যে এই সময় আমরা ক্রমাগত C যোগ করতে পারি না। এই ক্ষেত্রে অভিব্যক্তি নিম্নরূপ দেখায়:

এই ঘুরে ঘুরে যায়: মূলত, আমরা 3 এবং তারপর 2 অভিব্যক্তি প্রতিস্থাপিত এবং তাদের মধ্যে পার্থক্য প্রাপ্ত। এই ধ্রুবক

সি

আগের ব্যবহারের বিরোধিতা হিসাবে নির্দিষ্ট মান হয়

চলুন শুরু করা যাক ধ্রুবক ফ্যাক্টরটি (অনির্দিষ্ট অবিচ্ছেদ্যতার সাথে) আরও বিস্তারিতভাবে।

যদি y 3

3 এর ২ , ∫ 3y ^২ ডিএ = y এর পার্থক্য

3 যাইহোক, ^3y 2 ^{অনেক এক্সপ্রেশনগুলির মধ্যে পার্থক্য হতে পারে, যার মধ্যে রয়েছে}

y 3 ^-5 , > y 3 ⁺⁷ , ইত্যাদি … এইটি বোঝায় যে অপারেশন চলাকালে ধ্রুবকটি অকার্যকর হওয়ার পর বিপরীতটি অনন্য নয়। সাধারণভাবে 3y ² y

3 + সি ^{যেখানে} C কোন ধ্রুবক ঘটনাক্রমে, সি নামে পরিচিত হয় ^{'ইন্টিগ্রেশন এর ধ্রুবক'} আমরা এইভাবে লিখি: ∫ 3y 2 dx = y

3

+ সি ^{একটি অনির্দিষ্ট অবিচ্ছেদ্য জন্য ইন্টিগ্রেশন কৌশল, যেমন টেবিলের সন্ধান বা Risch ইন্টিগ্রেশন, ইন্টিগ্রেশন প্রক্রিয়ার সময় নতুন discontinuities যোগ করতে পারেন। এই নতুন বিচ্ছিন্নতাগুলি দেখা দেয় কারণ বিরোধী ডেরাইভেটিভগুলি জটিল লগারিদমগুলির প্রবর্তনের প্রয়োজন হতে পারে।} জটিল লগারিদমগুলির একটি ঝাঁঝা বিচ্ছিন্নতা থাকে যখন আর্গুমেন্ট নেগেটিভ রিয়েল অক্ষ অতিক্রম করে এবং একীকরণ অ্যালগরিদম কখনও কখনও একটি প্রতিনিধিত্ব খুঁজে পায় না যেখানে এই জাম্প বাতিল। ^{--২ ->} যদি নির্দিষ্ট অবিচ্ছেদ্য প্রথম কম্পিউটিং দ্বারা একটি অনির্দিষ্ট অবিচ্ছেদ্য মূল্যায়ন করা হয় এবং এর ফলে পরিণামে ইন্টিগ্রেশন সীমানাগুলি প্রতিস্থাপন করা হয়, তবে আমাদের সচেতন থাকতে হবে যে অনির্দিষ্ট একীকরণের অবতারণা সৃষ্টি হতে পারে। যদি এটি করে তবে অতিরিক্তভাবে, আমরা একীকরণের ব্যবধানের অসন্তোষগুলির তদন্ত করতে হবে।