বৈচিত্রিক এবং পার্থক্যর মধ্যে পার্থক্য

ডেরিভেটিভ বনাম ডিফারেনশিয়াল

ডিফারেনশিয়াল ক্যালকুলাসে, একটি ফাংশন এর ডেরিভেটিভ এবং ডিফারেনালের সাথে ঘনিষ্ঠভাবে সম্পর্কিত কিন্তু খুব ভিন্ন অর্থ রয়েছে এবং বিভিন্ন গুরুত্বপূর্ণ ফাংশন সম্পর্কিত দুটি গুরুত্বপূর্ণ গাণিতিক বস্তু প্রতিনিধিত্ব ব্যবহৃত।

ডেরিভেটিভ কি?

একটি ফাংশন ডেরিভেটিভ যার পরিমাণ তার ফাংশন মান হিসাবে তার ইনপুট পরিবর্তন হিসাবে পরিমাপ মাল্টি-ভেরিয়েবল ফাংশনগুলিতে, ফাংশন মানের পরিবর্তন স্বতন্ত্র ভেরিয়েবলগুলির মানগুলির পরিবর্তনের দিকের উপর নির্ভর করে। অতএব, এই ক্ষেত্রে, একটি নির্দিষ্ট দিক নির্বাচন করা হয় এবং ফাংশনটি নির্দিষ্ট নির্দেশে বিভেদ করা হয়। ডেরিভেটিভ ডাইরেক্টটিভ ডেসিভাল্টিভ আংশিক ডেরাইভেটিভস একটি বিশেষ ধরনের নির্দেশমূলক ডেরিভেটিভস।

একটি ভেক্টর-মূল্যবান ফাংশন এর ডেরিভেটিভ f সীমা হিসাবে সংজ্ঞায়িত করা যেতে পারে

যেখানেই থাকে সেখানে finitely যেমন আগে উল্লেখ করা হয়েছে, এটি আমাদেরকে f ভেক্টরের দিক দিয়ে উ একক মূল্যবান ফাংশনের ক্ষেত্রে, এটি ডেরাইভেটিভের সুপরিচিত সংজ্ঞা হ্রাস করে,

--২ ->

উদাহরণস্বরূপ,

সর্বত্র বদ্ধভোগী এবং ডেরিভেটিভ সীমা সমান,

, যা

এর সমান। ফাংশনের ডেরিভেটিভস যেমন

সর্বত্র বিদ্যমান তারা যথাক্রমে ফাংশন

এর সমান।

এই প্রথম ডেরিভেটিভ হিসাবে পরিচিত হয়। সাধারণত ফাংশন f প্রথম ডেরিভেটিভ f ⁽¹⁾ দ্বারা চিহ্নিত করা হয়। এখন এই নোট ব্যবহার করে, উচ্চ আদেশ ডেরাইভেটিভগুলি নির্ধারণ করা সম্ভব।

দ্বিতীয় ক্রম নির্দেশমূলক ডেরিভেটিভ এবং n ^ও ডেরাইভেটিভ দ্বারা f ⁽ⁿ⁾ প্রতিটি জন্য চিহ্নিত করা হয়েছে। n,

, n ^ও ডেরিভেটিভ

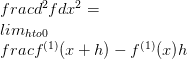
পার্থক্য কি?

একটি ফাংশন অফ ফাংশন ফাংশন এ পরিবর্তনকে স্বতন্ত্র ভেরিয়েবল বা ভেরিয়েবলের পরিবর্তনের প্রতিনিধিত্ব করে। f একটি একক ভেরিয়েবলের x, অর্ডার 1 df দ্বারা প্রদত্ত

দ্বারা দ্বারা প্রদত্ত ফাংশনের জন্য স্বাভাবিক অনুক্রমে। এর মানে হল যে x (অর্থাৎ d x) একটি অস্পষ্ট পরিবর্তনের জন্য ^f (1) (x <) d x পরিবর্তন f।

সীমা ব্যবহার করে এই সংজ্ঞাটি শেষ করতে পারে। অনুমান করুন Δ x পরিবর্তন x একটি অবাধ বিন্দুতে x এবং Δ f ফাংশনে সংশ্লিষ্ট পরিবর্তন চ । এটা দেখানো যেতে পারে যে Δ f = f ⁽¹⁾ (x) Δ x + ε, যেখানে ε হয় ভূল. এখন, সীমা Δ এক্স → 0 ^{Δ f} / _{Δ x} = f ^{(1) (} x) (ডেরিভেটিভের পূর্বে বর্ণিত সংজ্ঞা ব্যবহার করে) এবং এইভাবে, Δ x → 0 ε ^/ Δ _{x = 0অতএব, উপসংহারে বলা যায় যে, Δ x →} 0 ε = 0. এখন, denoting Δ x → 0 Δ f হিসাবে d f এবং Δ x → 0 Δ x হিসাবে d x ডিফারেন্স সংজ্ঞা কঠোরভাবে প্রাপ্ত হয় উদাহরণস্বরূপ, ফাংশন ডিফারেনশিয়াল হয়

।

দুই বা ততোধিক ভেরিয়েবলের ফাংশনের ক্ষেত্রে, প্রতিটি ফাংশনের মোট পার্থক্যটি স্বতন্ত্র ভেরিয়েবলের প্রতিটি দিকের ডিফারেনশনের সমষ্টি হিসাবে সংজ্ঞায়িত করা হয়। গাণিতিকভাবে, এটি হিসাবে উল্লেখ করা যেতে পারে

।

ডেরিভেটিভ এবং পার্থক্য মধ্যে পার্থক্য কি?

• ডেরিভেটিভ একটি ফাংশন পরিবর্তনের হার বোঝায় যখন ডিফারেনশিয়াল ফাংশন প্রকৃত পরিবর্তন বোঝায়, যখন স্বাধীন পরিবর্তনশীল পরিবর্তন সাপেক্ষে হয়।

• ডেরিভেটিভটি দ্বারা দেওয়া হয়, কিন্তু ডিফারেনশিয়াল দ্বারা দেওয়া হয় প্রস্তাবিত সুন্নী ও শিয়া ইসলামের মধ্যে পার্থক্য সুন্নী এবং শিয়া মধ্যে পার্থক্য সুইডেন ও সুইজারল্যান্ডের মধ্যে পার্থক্য