সমান্তরাল এবং রেম্বাসের মধ্যে পার্থক্য: সমান্তরাল বনাম র্যামবাস

সমান্তরাল বিভাজক বম্বস

সমান্তরাল এবং রম্বস চতুর্ভুজ হাজার হাজার বছর ধরে মানুষের কাছে এই পরিসংখ্যানগুলির জ্যামিতি পরিচিত ছিল। গ্রিক গণিতবিদ ইউক্লিডের লেখা বই "এলিয়েমেন্টস" বইটি স্পষ্টভাবে বিবেচনা করা হয়।

সমান্তরাল সার্টিফিকেট

সমান্তরাল সারফেস চারপাশের জ্যামিতিক চিত্র হিসাবে সংজ্ঞায়িত করা যেতে পারে, একে অপরের সাথে বিপরীত দিকে সমান্তরাল। আরও সুস্পষ্টভাবে এটি সমান্তরাল পার্শ্ব দুটি জোড়া সঙ্গে একটি চতুর্ভুজ হয়। এই সমান্তরাল প্রকৃতি parallelograms অনেক জ্যামিতিক বৈশিষ্ট্য দেয়।

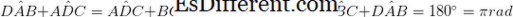
জ্যামিতিক বৈশিষ্ট্যগুলি পাওয়া গেলে একটি চতুর্ভুজ একটি সমান্তরাল হয়।

• প্রতিপক্ষের দ্বৈত দৈর্ঘ্যের সমান। (এবি = ডিসি, এডি = বিসি)

• প্রতি কোণে কোণের দুই জোড়া সমান আকার। (

)

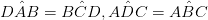
• যদি সংলগ্ন কোণ সম্পূরক হয়

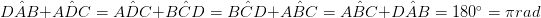
• পাশের একটি জোড়া, যা একে অপরকে বিরোধ করছে, সমান্তরাল এবং দৈর্ঘ্য সমান। (এবি = ডিসি এবং AB∥DC)

• তীরগুলি একে অপরকে বিভক্ত করে (AO = OC, BO = OD)

• প্রতিটি তির্যক চতুর্ভুজকে দুটি সমান্তরাল ত্রিভূজের মধ্যে বিভক্ত করে। (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

আরও, পাশের স্কোয়ারগুলির সমান ত্রিপুরাগুলির সমষ্টি সমান। এই কখনও কখনও সমান্তরাল আইন [999] হিসাবে উল্লেখ করা হয় এবং পদার্থবিদ্যা এবং প্রকৌশল ব্যাপক অ্যাপ্লিকেশন আছে (এবি ২ ^{+ বিসি} ২ ^{+ সিডি} ২ ^{+ ডিএ} ২ ^{= এসি} ২ ^{+ বিডি} 2 ⁾ উপরোক্ত বৈশিষ্ট্যের প্রতিটিটি বৈশিষ্ট্য হিসাবে ব্যবহার করা যেতে পারে, একবার এটি প্রতিষ্ঠিত হওয়ার পর যে চতুর্ভুজ একটি সমান্তরাল হয়।

সমান্তরাল সারফেসের আয়তন এক পাশের দৈর্ঘ্য এবং উচ্চতাটি বিপরীত দিকে থেকে গণনা করা যেতে পারে। অতএব, সমান্তরাল চক্রের এলাকা

সমান্তরাল = ক্ষেত্রের গড় = উচ্চতা = এবি × এইচ

সমান্তরাল অঞ্চলটি পৃথক সমান্তরাল চক্র আকারের স্বাধীন। এটি কেবল দৈর্ঘ্যের এবং ঋজু উচ্চতার উপর নির্ভরশীল।

যদি সমান্তরাল উভয় পক্ষের দুই ভেক্টর দ্বারা প্রতিনিধিত্ব করা যায়, তবে এলাকাটি দুটি সন্নিহিত ভেক্টর ভেক্টর পণ্য (ক্রস পণ্য) এর মাত্রা দ্বারা প্রাপ্ত করা যেতে পারে।

যদি পক্ষ AB এবং AD যথাক্রমে ভেক্টর () এবং (

) দ্বারা প্রতিনিধিত্ব করে, সমান্তরালকরণের এলাকাটি

দ্বারা প্রদান করা হয়, যেখানে α হলো

এবং এর মধ্যে কোণ >।

প্যারাললোগ্রামের কিছু উন্নত বৈশিষ্ট্য নিম্নরূপ;

• একটি সমান্তরাল খণ্ডের ক্ষেত্রটি তার ত্রিভুজগুলির কোনটি দ্বারা নির্মিত ত্রিভূজের দ্বিগুণ ক্ষেত্র।

• সমান্তরাল সংখ্যাটি মধ্যপার্শ্বের মধ্য দিয়ে প্রবাহিত কোন লাইনের অর্ধেক অংশে বিভক্ত।

• কোনও অপ্রচলিত affine রূপান্তর অন্য parallelogram

একটি সমান্তরাল চক্র লাগে - একটি সমান্তরাল ক্রম 2 এর ক্রমবিন্যাস সমীকরণ [2 999] • পক্ষের একটি সমান্তরাল ক্রোমের কোন অভ্যন্তরীণ বিন্দু থেকে দূরত্ব স্বাধীন বিন্দুর অবস্থান

রম্বস

সমস্ত চতুর্থাংশের একটি চতুর্ভুজ সমান লম্বা সমান একটি সমাধি হিসাবে পরিচিত হয়। এটি একটি

সামঞ্জস্যপূর্ণ চতুর্ভুজ

হিসাবে নামকরণ করা হয়। এটি একটি হীরক আকৃতি বলে মনে করা হয়, খেলোয়াড়ী কার্ডগুলির মধ্যে একের মত।

রম্বস এছাড়াও সমান্তরালogram এর একটি বিশেষ কেস। এটি সমতুল্য হিসাবে বিবেচনা করা যেতে পারে চারটি সমান সমান। এবং এটি একটি বিশেষ বৈশিষ্ট্য আছে, একটি সমান্তরালogram এর বৈশিষ্ট্য ছাড়াও। • সমাকলির তীরচিহ্নগুলি একে অপরের ডান কোণে বিভক্ত; আয়তক্ষেত্র লম্বা হয়। • দেওয়াল দুটি বিপরীত অভ্যন্তরীণ কোণগুলিকে বিভক্ত করে।

• সন্নিহিত পক্ষগুলির কমপক্ষে দুটি দৈর্ঘ্যের সমান।

সমান্তরাল ক্রোমের সমতুল্য হিসাবে একই পদ্ধতিতে রম্বসের এলাকা গণনা করা যেতে পারে।

সমান্তরালogram এবং র্যামম্বাসের মধ্যে পার্থক্য কি?

• সমান্তরাল এবং সমম্বল চতুর্ভুজ Rhombus হল প্যারালালোগ্রামের একটি বিশেষ কেস।

• ফর্মুলার বেস × উচ্চতা ব্যবহার করে যে কোনও এলাকার গণনা করা যায়।

• দেওয়ালগুলি বিবেচনা করা;

- সমান্তরাল তীরগুলির একে অপরকে বিভাজক করে এবং সমান্তরাল সমান্তরাল দুটি সমান্তরাল ত্রিভুজ গঠন করে।

- সমকোণী কোণের তীরচিহ্নগুলি একে অপরের কোণে বিভক্ত করে এবং ত্রিভুজ গঠিত সমানুপাতিক।

• অভ্যন্তরীণ কোণ বিবেচনা;

- সমান্তরাল সমমানের অভ্যন্তরীণ কোণগুলি সমান আকারের সমান। দুটি সংলগ্ন অভ্যন্তরীণ কোণ সম্পূরক।

- রম্বসের অভ্যন্তরীণ কোণগুলির দ্বারগুলি দ্বারা বিভাজ করা হয়।

• পক্ষগুলি বিবেচনা করা;

- একটি সমান্তরাল সারিতে, ত্রিভুজগুলির সমতুল্য সমান্তরাল (সমান্তরাল আইন) -এর সমান সমান বিন্দুর সমান।

- যেহেতু সব চারপাশে সমান্তরাল সমীকরণের সমান হয়, ত্রিভুজটির চতুর্ভুজের সমান সমান চার বার সমান।