পাওয়ার সিরিজ এবং টেলর সিরিজ মধ্যে পার্থক্য
পাওয়ার সিরিজ বনাম টেলর সিরিজ
গণনাতে, একটি বাস্তব অনুক্রম বাস্তব সংখ্যাগুলির একটি অর্ডার তালিকা। । আনুষ্ঠানিকভাবে, এটি প্রকৃত সংখ্যার সেট থেকে একটি প্রকৃত সংখ্যা সেট থেকে একটি ফাংশন। যদি একটি n হয় n ও একটি ক্রম শব্দ, আমরা ক্রম দ্বারা বা একটি 1 , 2 , …, একটি n, …। উদাহরণস্বরূপ, ক্রম 1, ½, ⅓, …, 1 / n , … বিবেচনা করুন। এটি {1 / n} হিসাবে চিহ্নিত করা যেতে পারে।
শৃঙ্খলা ব্যবহার করে একটি সিরিজ নির্ধারণ করা সম্ভব। একটি সিরিজ একটি ক্রম পদ সমষ্টি হয়। অতএব, প্রতিটি ক্রম জন্য, একটি সংযুক্ত ক্রম এবং ভাইস-বিপরীত হয়। যদি {a n} বিবেচনা অনুসারে ক্রম হয়, তাহলে, এই অনুক্রম দ্বারা গঠিত সিরিজটি প্রতিনিধিত্ব করা যেতে পারে:
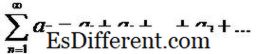
সুতরাং, উপরের উদাহরণে, সংশ্লিষ্ট সিরিজ 1+ 1 / 2 + 1 / 3 + … + 1 / n + …
নামগুলি সুপারিশ হিসাবে, পাওয়ার সিরিজ একটি বিশেষ ধরনের সিরিজ এবং এটি সংখ্যাসূচক বিশ্লেষণ এবং সম্পর্কিত গাণিতিক মডেলিং ব্যাপকভাবে ব্যবহৃত হয়। টেলর সিরিজ একটি বিশেষ শক্তি সিরিজ যা সুবিন্যস্ত ফাংশন প্রতিনিধিত্বমূলক একটি বিকল্প এবং সহজ-থেকে-ম্যানিপুলেট উপায় প্রদান করে।
পাওয়ার সিরিজ কি?
একটি শক্তি সিরিজ ফর্ম একটি সিরিজ

বাস্তব বা জটিল সংখ্যা হতে পারে, এবং x; আমি। ঙ। ডামি পরিবর্তনশীল উদাহরণস্বরূপ, একটি n = 1 for each n, এবং c = 0, ক্ষমতা সিরিজ 1 + x + x সেটিং দ্বারা 2 + … + এক্স n + … পাওয়া যায়। এটি লক্ষ্য করা সহজ যে যখন x ε (-1, 1), এই শক্তি সিরিজ 1 / (1-x) রূপান্তরিত হয়। --২ ->
একটি শক্তি সিরিজ যখনx = c এর সমরূপ হয়। x এর অন্যান্য মানগুলি যার জন্য বিদ্যুৎ সিরিজ সংকুচিত হয় সবসময় c এ কেন্দ্রীভূত একটি খোলা ব্যবধানের আকার গ্রহণ করবে। যে, একটি মান হবে 0≤ R ≤ ∞ যেমন প্রতিটি জন্য এক্স সন্তোষজনক | xc | ≤ R, পাওয়ার সিরিজ সমরূপ এবং প্রতিটি এক্স সন্তুষ্ট | xc |> R, পাওয়ার সিরিজ ভিন্ন। এই মান R ক্ষমতা সিরিজের কনভারজেন্সের ব্যাসার্ধ (R কোনও প্রকৃত মূল্য বা ইতিবাচক অ্যান্টিফট নিতে পারে) বলে।
তারপর,


আমি। ঙ।
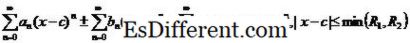
টেলর সিরিজ কি? টেলর সিরিজ একটি ফাংশন

f
(x) জন্য নির্ধারিত হয় যা একটি ব্যবধানে অসীমভাবে ভিন্নতর। অনুমান করুন f (x) c এ কেন্দ্রীভূত একটি ব্যবধানের উপর নির্ভরযোগ্য। তারপর যে শক্তি সিরিজ

(x) সম্পর্কে c এর টেলর সিরিজ সম্প্রসারণ বলা হয়। (n) (c ) ও এক্স = ডেরিভেটিভকে নির্দেশ করে। গ)। সংখ্যাসূচক বিশ্লেষণে, এই অসীম সম্প্রসারণের একটি সীমিত সংখ্যার গুণগুলি মূল্যের হিসাবের জন্য ব্যবহার করা হয় যেখানে সিরিজ মূল ফাংশনের সাথে সমান হয়। একটি ফাংশন f
(x) ব্যবধান (a, b) এ বিশ্লেষণাত্মক বলে মনে করা হয়, যদি প্রতিটি x ε (a, b)), টেলার সিরিজ f (x) ফাংশন f (x) এ রূপান্তর করে। উদাহরণস্বরূপ, 1 / (1-x) হল বিশ্লেষণাত্মক (-1, 1), যেহেতু তার টেলার সম্প্রসারণ 1 + x + x 2 + … + x n + … রূপান্তরিত হয় ই এক্স রূপান্তর ই x x প্রতিটি বাস্তব সংখ্যার জন্য x পাওয়ার সিরিজ এবং টেলর সিরিজের মধ্যে পার্থক্য কি? 1। টেলর সিরিজ একটি বিশেষ বর্গ শক্তি সিরিজ শুধুমাত্র কিছু খোলা ব্যবধানে infinitely differentiable যা ফাংশন জন্য সংজ্ঞায়িত।
2। টেলর সিরিজ বিশেষ ফর্ম গ্রহণ করে
তবে, একটি শক্তি সিরিজফর্মের কোন সিরিজ হতে পারে! --2 ->




