আয়তক্ষেত্র এবং Rhombus মধ্যে পার্থক্য: আয়তক্ষেত্র বনাম র্যাম্বস
আয়তক্ষেত্র বনাম রম্বস
রম্বস এবং আয়তক্ষেত্র চতুর্ভুজ হাজার হাজার বছর ধরে মানুষের কাছে এই পরিসংখ্যানগুলির জ্যামিতি পরিচিত ছিল। গ্রিক গণিতবিদ ইউক্লিডের লেখা বই "এলিয়েমেন্টস" বইটি স্পষ্টভাবে বিবেচনা করা হয়।
সমান্তরাল সার্টিফিকেট
সমান্তরাল সারফেস চারপাশের জ্যামিতিক চিত্র হিসাবে সংজ্ঞায়িত করা যেতে পারে, একে অপরের সাথে বিপরীত দিকে সমান্তরাল। আরও সুস্পষ্টভাবে এটি সমান্তরাল পার্শ্ব দুটি জোড়া সঙ্গে একটি চতুর্ভুজ হয়। এই সমান্তরাল প্রকৃতি parallelograms অনেক জ্যামিতিক বৈশিষ্ট্য দেয়।


জ্যামিতিক বৈশিষ্ট্যগুলি পাওয়া গেলে একটি চতুর্ভুজ একটি সমান্তরাল হয়।
• প্রতিপক্ষের দ্বৈত দৈর্ঘ্যের সমান। (এবি = ডিসি, এডি = বিসি)
• প্রতি কোণে কোণের দুই জোড়া সমান আকার। (

• যদি সংলগ্ন কোণ সম্পূরক হয়

• পাশের একটি জোড়া, যা একে অপরকে বিরোধ করছে, সমান্তরাল এবং দৈর্ঘ্য সমান। (এবি = ডিসি এবং AB∥DC)
• তীরগুলি একে অপরকে বিভক্ত করে (AO = OC, BO = OD)
• প্রতিটি তির্যক চতুর্ভুজকে দুটি সমান্তরাল ত্রিভূজের মধ্যে বিভক্ত করে। (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)
আরও, পাশের স্কোয়ারগুলির সমান ত্রিপুরাগুলির সমষ্টি সমান। এই কখনও কখনও সমান্তরাল আইন [999] হিসাবে উল্লেখ করা হয় এবং পদার্থবিজ্ঞান এবং প্রকৌশল ব্যাপক অ্যাপ্লিকেশন আছে (এবি ২ + বিসি ২ + সিডি ২ + ডিএ ২ = এসি ২ + বিডি 2 ) উপরোক্ত বৈশিষ্ট্যের প্রতিটিটি বৈশিষ্ট্য হিসাবে ব্যবহার করা যেতে পারে, একবার এটি প্রতিষ্ঠিত হওয়ার পর যে চতুর্ভুজ একটি সমান্তরাল হয়।
সমান্তরাল সারফেসের আয়তন এক পাশের দৈর্ঘ্য এবং উচ্চতার বিপরীত পার্শ্বের গণনা করা যেতে পারে। অতএব, সমান্তরাল চক্রের এলাকা
সমান্তরাল = ক্ষেত্রের গড় = উচ্চতা =
এবি × h সমান্তরাল অঞ্চলটি পৃথক সমান্তরাল চক্রের আকার থেকে স্বাধীন বলে উল্লেখ করা যেতে পারে। এটি কেবল দৈর্ঘ্যের এবং ঋজু উচ্চতার উপর নির্ভরশীল।

যদি সমান্তরাল উভয় পক্ষের দুই ভেক্টর দ্বারা প্রতিনিধিত্ব করা যায়, তাহলে এলাকাটি দুটি সন্নিহিত ভেক্টর ভেক্টর পণ্য (ক্রস পণ্য) এর মাত্রা দ্বারা প্রাপ্ত করা যেতে পারে।
যদি পক্ষ AB এবং AD যথাক্রমে ভেক্টর () এবং (
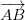
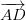

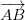
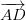
• সমান্তরাল সংখ্যাটি মধ্যপার্শ্বের মধ্য দিয়ে প্রবাহিত কোন লাইনের অর্ধেক অংশে বিভক্ত।
• কোনও অপ্রচলিত affine রূপান্তর অন্য parallelogram
একটি সমান্তরাল চক্র লাগে - একটি সমান্তরাল ক্রম 2 এর ক্রমবিন্যাস সমীকরণ [2 999] • পক্ষের একটি সমান্তরাল ক্রোমের কোন অভ্যন্তরীণ বিন্দু থেকে দূরত্ব স্বাধীন পয়েন্টের অবস্থান
আয়তক্ষেত্র
চারটি ডান কোণের সাথে চতুর্ভুজ একটি আয়তক্ষেত্র হিসাবে পরিচিত। এটি সমান্তরাল সার্টিফিকেটের একটি বিশেষ কেস যেখানে কোন দুটি সন্নিহিত দিকের কোণগুলি ডান দিকের কোণ।
একটি সমান্তরাল সারির সমস্ত বৈশিষ্ট্য ছাড়াও, আয়তক্ষেত্রের জ্যামিতি বিবেচনা করার সময় অতিরিক্ত বৈশিষ্ট্যগুলি স্বীকৃত হতে পারে।
• কোণে প্রতিটি কোণ একটি ডান কোণ হয়।
• তির্যক দৈর্ঘ্য সমান, এবং তারা একে অপরকে বিভক্ত করে। অতএব, বিজড়িত অংশের দৈর্ঘ্য সমান হয়।

• পাইথাগোরস থিওরেম ব্যবহার করে তির্যক দৈর্ঘ্য গণনা করা যেতে পারে:
পিকিউ
2
+ পিএস
২ = SQ 2 এলাকা সূত্র দৈর্ঘ্য এবং প্রস্থের পণ্য হ্রাস। আয়তক্ষেত্রের দৈর্ঘ্য × দৈর্ঘ্য × প্রস্থের • অনেক আয়তক্ষেত্রের বৈশিষ্ট্য একটি আয়তক্ষেত্র পাওয়া যায়, যেমন;
- একটি আয়তক্ষেত্র চক্রাকার, যেখানে সমস্ত বৃত্ত একটি বৃত্তের ঘেরের উপর স্থাপিত হতে পারে।
- এটি সমানুপাতিক, যেখানে সমস্ত কোণ সমান।
- এটি সমতুল্য, যেখানে সমস্ত কোণ একই সমতাবিশিষ্ট কক্ষপথের মধ্যে অবস্থিত।
- উভয় প্রতিবিম্ব সমীকরণ এবং ঘূর্ণনশীল সমাহার উভয় আছে।
রম্বস
সমস্ত চতুর্দিকে একটি চতুর্ভুজ একটি দৈর্ঘ্য সমান একটি সমাধি হিসাবে পরিচিত হয়। এটি একটি
সামঞ্জস্যপূর্ণ চতুর্ভুজ
হিসাবে নামকরণ করা হয়। এটি একটি হীরক আকৃতি বলে মনে করা হয়, খেলোয়াড়ী কার্ডগুলির মধ্যে একের মত।
রম্বস এছাড়াও সমান্তরালogram এর একটি বিশেষ কেস। এটি সমতুল্য হিসাবে বিবেচনা করা যেতে পারে চারটি সমান সমান। এবং এটি একটি বিশেষ বৈশিষ্ট্য আছে, একটি সমান্তরালogram এর বৈশিষ্ট্য ছাড়াও। • সমাকলির তীরচিহ্নগুলি একে অপরের ডান কোণে বিভক্ত; আয়তক্ষেত্র লম্বা হয়। • দেওয়াল দুটি বিপরীত অভ্যন্তরীণ কোণগুলিকে বিভক্ত করে।

• সন্নিহিত পক্ষগুলির কমপক্ষে দুটি দৈর্ঘ্যের সমান।
সমান্তরাল ক্রোমের সমতুল্য হিসাবে একই পদ্ধতিতে রম্বসের এলাকা গণনা করা যেতে পারে।
Rhombus এবং Rectangle মধ্যে পার্থক্য কি?
• রম্বস এবং আয়তক্ষেত্র হল চতুর্ভুজ। আয়তক্ষেত্র এবং সমম্বয় সমান্তরাল বিশেষ বিশেষ ক্ষেত্রে।
• ফর্মুলা
বেস × উচ্চতা
ব্যবহার করে যে কোনও এলাকা গণনা করা যায়।
• দেওয়ালগুলি বিবেচনা করা; - সমকোণী কোণের তীরচিহ্নগুলি একে অপরের কোণে বিভক্ত করে এবং ত্রিভুজ গঠিত সমানুপাতিক। - আয়তক্ষেত্রের তীরগুলি দৈর্ঘ্য সমান এবং একে অপরকে বিভক্ত; বিজড়িত অংশের দৈর্ঘ্য সমান। আয়তক্ষেত্রটি দুটি সমান্তরাল ডান ত্রিভূজের মধ্যে বিভাজক বিভাজক।
• অভ্যন্তরীণ কোণ বিবেচনা;
- রম্বসের অভ্যন্তরীণ কোণগুলি দ্বারগুলির দ্বারা বিভক্ত হয়
- আয়তক্ষেত্রের চারটি অভ্যন্তরীণ কোণগুলি সঠিক কোণ।
• পক্ষগুলি বিবেচনা করা;
- যেহেতু সব চারপাশে সমান্তরাল সমীকরণে সমান হয়, ততক্ষণ চতুর্ভুজের চতুর্ভুজের সমান তীরবর্তী বর্গাকার সমতুল্য (সমান্তরাল লৌকিক আইন ব্যবহার করে)
- আয়তক্ষেত্রে, বর্গক্ষেত্রের সমষ্টি উভয় সন্নিহিত পক্ষ সমান তীরের বর্গক্ষেত্রের সমান।(পাইথগোর্স 'রুল)




